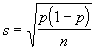
Schätzverfahren: Beim Schätzen gehen wir in ähnlicher Weise vor. Nehmen wir wieder eine Stichprobe F mit n = 1.000 an, in der wir diesmal 400 G gefunden haben. Das ergibt eine Proportion P von G in F in Höhe von 40% oder 0,4. In welchem Intervall wird mit welcher Wahrscheinlichkeit der p-Wert der Grundgesamtheit liegen? Da wir wissen, daß die Stichprobenproportionen von Stichproben gleichen Umfangs in einen von p abhängigen Bereich fallen, können wir diese Kenntnis für die Bestimmung eines Konfidenzintervalls ausnutzen. Wir wissen das wegen der bei der gegebenen Stichprobengröße möglichen Anwendung der Normalverteilung. Da fallen dann 95% der Stichprobenproportionen in den durch p - 1,96 Standardabweichungen und den durch p + 1,96 Standardabweichungen abgesteckten Bereich. Mathematisch kann man das so ausdrücken:
Nun können wir alle die möglichen Werte für den unbekannten Parameter p, bei denen das Stichprobenergebnis P noch zu den 95% der unter p zu erwartenden Stichprobenergebnisse gehört, durch eine einfache Umformung erhalten:
Für alle p, die dieser Bedingung genügen, gehört der empirische Befund P zum ,,mittleren Bereich", der insgesamt eine Wahrscheinlichkeit von 95% hat. Wir müssen jetzt noch das s bestimmen. Das geht bei der Formel
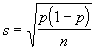
für Proportionen in binomialverteilten Grundgesamtheiten auf zwei Wegen. Der eine führt ebenfalls zu einer Schätzung, indem er in die Formel an die Stelle des unbekannten p-Wertes der Grundgesamtheit die bekannte Proportion P der Stichprobe setzt. Das soll erlaubt sein, wenn n größer ist als 9 geteilt durch P(1 - P) (vgl. Clauss/Ebner Grundlagen der Statistik, 1971, S. 160). Der andere legt einfach den größtmöglichen Wert von p(1 - p) zugrunde. Der beträgt höchstens 0,25, so daß die Standardabweichung s höchstens den Wert der Wurzel aus (0,25 geteilt durch n) annimmt. Bei diesem Weg ist das Konfidenzintervall auf dem Niveau von 95% ermittelt durch
Die Länge des Konfidenzintervalls, also der Spielraum für die in
Betracht zu ziehenden Werte für p beträgt beim Niveau von 95% gerade
![]() und beim Niveau von 99% gerade
und beim Niveau von 99% gerade
![]() . Deutlich wird bei dieser
Entwicklung, daß das Intervall mit wachsendem n immer kleiner wird. Die
Schätzsicherheit hängt deshalb von der Größe der Stichprobe
ab. Für unsere Beispielsstichprobe können wir mit einer Sicherheit von
95% sagen, daß der p-Wert der Grundgesamtheit in dem Intervall von 0,37
bis 0,43 liegt, und mit einer Sicherheit von 99%, daß er in dem Intervall
von 0,36 bis 0,44 liegt. Wären die G die von den durch eine Werbung
angesprochenen Verkehrskreise F Getäuschten (vgl. oben
RN 7), hätten wir bei diesem Stichprobenergebnis
keine Probleme, einen nicht unerheblichen Anteil (nämlich mehr als 10%) als
irregeführt anzusehen. Bei der Stichprobengröße von 10 kämen
wir allerdings in erhebliche Schwierigkeiten. Die wegen der geringen Größe
der Stichprobe allerdings problematische Anwendung der aus der Normalverteilung
gewonnenen Formel ergäbe selbst bei einem Vertrauensniveau von 95% ein
Intervall von 0,09 bis 7,1, das auch einen Anteil der Irregeführten unter
10% möglich macht.
. Deutlich wird bei dieser
Entwicklung, daß das Intervall mit wachsendem n immer kleiner wird. Die
Schätzsicherheit hängt deshalb von der Größe der Stichprobe
ab. Für unsere Beispielsstichprobe können wir mit einer Sicherheit von
95% sagen, daß der p-Wert der Grundgesamtheit in dem Intervall von 0,37
bis 0,43 liegt, und mit einer Sicherheit von 99%, daß er in dem Intervall
von 0,36 bis 0,44 liegt. Wären die G die von den durch eine Werbung
angesprochenen Verkehrskreise F Getäuschten (vgl. oben
RN 7), hätten wir bei diesem Stichprobenergebnis
keine Probleme, einen nicht unerheblichen Anteil (nämlich mehr als 10%) als
irregeführt anzusehen. Bei der Stichprobengröße von 10 kämen
wir allerdings in erhebliche Schwierigkeiten. Die wegen der geringen Größe
der Stichprobe allerdings problematische Anwendung der aus der Normalverteilung
gewonnenen Formel ergäbe selbst bei einem Vertrauensniveau von 95% ein
Intervall von 0,09 bis 7,1, das auch einen Anteil der Irregeführten unter
10% möglich macht.
![]() vorherige
Randnummer
vorherige
Randnummer
![]() nächste
Randnummer
nächste
Randnummer